| Index | Thell | Documents | Links | About |
このページでは、リバーシプログラムThellの思考エンジン"spot"で使われているアルゴリズムについて解説します。リバーシプログラミングについてある程度の理解と経験があることを前提としていますので、初めての方は参考文献にあるような文書を参照することから始めるとよいでしょう。
ThellのボードはBoardというクラスです。このクラスは非常に大規模で高機能なクラスですが、ボード本体はColor型(実体はint)の2次元配列となっています。
ボードの設計において大きな論点となるのがmove/undoの実装です。ゲーム木探索では深さ優先で着手と取り消しを頻繁に行うため、この処理をいかに高速に行うかが重要になってきます。1つは、着手時にボードのコピーを生成してコピーに対して着手操作を行い、取り消し時にはコピーを破棄するコピー方式。もう1つは着手に際して変更点を記録してスタックに積み、取り消し時にはスタックの履歴を元に変更点だけを書き戻す差分方式。前者ではコピーにかかるコストが、後者ではスタック操作にかかるコストが問題となります。
Thellでは、差分方式を採用しています。これは、1回の着手で書き換わる箇所はそれほど多くないため、ボード全体をコピーするよりも差分を取った方が処理が軽いだろうという判断に依ります。
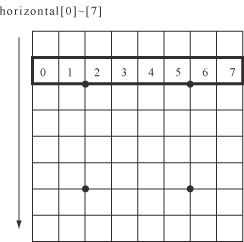
近年のリバーシプログラミング業界で常識となっている手法にインデックスの利用があります。これは、辺の石の配置などを符号化して一意の整数値で表現する手法です。例えば水平方向の一辺の8石の並びを考えた場合、それぞれのマスについて黒、白、空きの3通りの場合があるので、3^8 = 6561通りの整数で各々の配置を符号化できることになります。
例えば、水平辺の2番目、horizontal[1]は以下のような辺を表しており、0,1,2...と示したマスの色に対してblack = 2, empty = 1, white = 0で符号化を行い、i番目(i=0,...,7)のマスの符号に対して3のi乗をかけて加えた数がインデックスです。

インデックスを用いると何がうれしいかというと、リバーシの盤面操作に絡むアルゴリズムは各々の辺について独立であることが多く、操作結果を事前に計算しておいて表に格納しておき、辺のインデックスから結果だけを取ってくる、という操作が可能になることです。
Thellでは、Indexerというクラスがボードのインデックスを保持しています。インデックスは、水平*8個、垂直*8個、斜め辺*11個が2方向、の合計38個です。斜め辺が11個なのは、長さ1と長さ2の斜め辺は着手に関係ない(この方向に石を挟んで返すことはできない)ため、省いていることによります。長さが8に満たない斜め辺の場合は、マスが存在しない箇所を空マスと見なすことによって、水平・垂直辺の場合と同様に着手可能かどうかを調べられるようにしています。
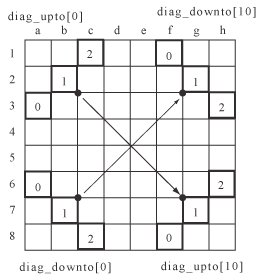
着手によって石が返ったときは、影響を受ける(値が変化する)インデックスについてのみ、差分を計算してインデックス値を更新します。
着手に際して、インデックスを利用します。どの方向に何個石が返せるか、返せないかは実際に8方向を調べてみないとわからないわけですが、これは辺ごとに独立に調べることができるため、全ての石の並び方についてどこに石を置いたら何石返せるかを事前に調べて表にしておくことができます。これが着手可能表(mobility table)です。辺の石の並び方は高々3^8 = 6561通りなので、表の構築は一瞬でできます。
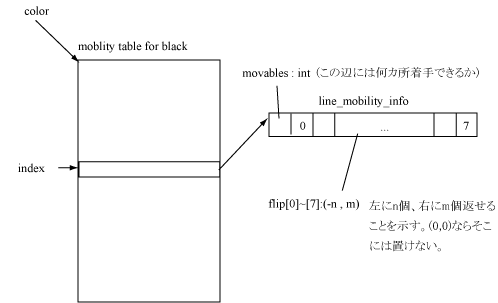
つまり、着手可能かどうか調べるには、8方向について
を調べればよいことになります。
(そのまま実装/bitboard)
以前のspotのボードの実装では、STLのvectorを多用した構造になっていました。現在はこれを自分で作った簡易vectorクラスに置き換えています。それは、少なくともVisual C++ .NET 2003に付属するSTLの実装は腐っており、clear()時にメモリを解放するため、重すぎて使っていられないためです。clear()ではメモリを解放しないように決まっているはずですが……。
探索アルゴリズムには、反復深化するnegamax版alpha-betaを用いています。探索木の根に近い方では、PVS(Pricipal Variation Search)を使っています。
PVSはnull window searchを行って処理の高速化を図る点でNegaScoutと本質的には同じですが、「alpha-beta windowを満たす値(principal variation)を見つけるまではnull window searchを行わない」という部分が違いでしょうか。子ノードは最善手順にmove orderingされているという前提のもと、principal variationを見つけた後はnull window searchによってprincipal variationより悪いことのみを確認します。もちろんmove orderingが常に完璧とは限りませんから、principal variation発見後にそれ以降のノードでよりよい値を発見する可能性があります。その場合は、null window searchのみでは不十分で、windowを本来の幅にして最探索を行います。そのあたりの仕組みはNegaScoutと全く同じです。
単純なalpha-betaとPVSの性能差について簡単な比較測定をしてみました。(Pentium4 3GHzにおける測定)
| アルゴリズム | 内部ノード数 | 葉ノード数 | 全探索ノード数 | 時間(秒) |
|---|---|---|---|---|
| alpha-beta | 8,874,253 (1.0) | 16,330,773 (1.0) | 25,205,026 (1.0) | 23.36 (1.0) |
| PVS | 7,214,182 (0.81) | 12,656,360 (0.78) | 19,870,542 (0.79) | 19.938 (0.85) |
| アルゴリズム | 内部ノード数 | 葉ノード数 | 全探索ノード数 | 時間(秒) |
|---|---|---|---|---|
| alpha-beta | 20,889,941 (1.0) | 7,110,837 (1.0) | 28,000,778 (1.0) | 13.906 (1.0) |
| PVS | 18,670,966 (0.89) | 6,338,665 (0.89) | 25,009,631 (0.89) | 11.718 (0.84) |
| アルゴリズム | 内部ノード数 | 葉ノード数 | 全探索ノード数 | 時間(秒) |
|---|---|---|---|---|
| alpha-beta | 60,288,739 (1.0) | 20,688,886 (1.0) | 80,977,625 (1.0) | 40.656 (1.0) |
| PVS | 37,243,908 (0.62) | 12,446,931 (0.60) | 49,690,839 (0.61) | 25.625 (0.63) |
| アルゴリズム | 内部ノード数 | 葉ノード数 | 全探索ノード数 | 時間(秒) |
|---|---|---|---|---|
| alpha-beta | 82,945,965 (1.0) | 28,375,754 (1.0) | 111,321,719 (1.0) | 52.219 (1.0) |
| PVS | 43,904,598 (0.53) | 14,822,248 (0.54) | 58,726,846 (0.53) | 28.203 (0.54) |
括弧内の数値は、alpha-betaによる値を1.0としたときのPVSの値を表します。PVSの採用によって中盤では約15%、終盤では15〜45%近く探索時間を短縮できています。
alpha-beta探索が単純なminimax探索に対して性能を上げられるのは、よい枝から順に探索を行ったときです。逆に悪い枝から順に評価した場合はminimaxと同じ性能しか得られません。このため、探索速度を上げるためには枝を評価する順番がきわめて重要です。この並び替えをmove orderingと言います。
Thellでは、反復深化をうまく利用して手を並べ替えています。具体的には、置換表(後述)を2枚用意しておき、片方に前回(一段浅い探索)の探索における置換表を入れ、もう片方を今回の探索の置換表として使います。
前回の置換表に存在している局面は、前回枝刈りされなかった局面であり、よい手である可能性が高い局面です。従って、前回の置換表に存在する局面から優先して探索を行います。前回の置換表に存在しなかった局面については、静的評価関数による評価値で並べ替えておきます。
move orderingに用いる静的評価関数は、序盤〜中盤では評価関数そのもの、終盤では速さ優先探索(後述)のために着手可能手数を数える関数としています。
move orderingの実装はAlphaBetaAI::sort(AI.cpp)にあります。
反復深化のアルゴリズムは以下のようになります。実装はAlphaBetaAI::moveMidGame及びAlphaBetaAI::moveEndGame(ともにAI.cpp)にあります。
置換表A(前回用), B(今回用)を用意;
int d = 初期値; // 4とか
do {
alphabeta(d, -∞, +∞);
swap (A, B); // 置換表の役割を交換
d++;
} while (d <= 最終的な先読み手数);
終盤はコンピュータリバーシが最も得意とする分野です。終盤完全読み切りは(正しく実装されていれば)「絶対に手を間違うことがない」ため、深い終盤読み切りを高速で行えることは強さに直結します。spotは、終盤では以下のような工夫によって探索速度を上げています。
move orderingや置換表による枝刈りは探索ノード数を減少させますが、その分余計なコストがかかります。ゲーム木の葉に近い部分では、move orderingのコストが枝刈りによって削減できる時間的コストを上回る場合もあります。このため、葉から一定の高さ以内にあるノードではmove orderingや置換表への登録・検索を行わないようにして、探索速度を上げています。この高さとして、中盤では3、終盤では7を用いています。これらは実験的に決定された値で、評価関数やボード表現の実装によって多少上下します。
なお、spotではこの切り替え地点を境にPVSと単純alpha-betaを切り替えています。すなわち、
のように探索手法を組み合わせて高速化をはかります。
探索アルゴリズムはとにかく高速であればあるほど望ましいのは言うまでもありません。試合によっては持ち時間が制限されている場合もあり、探索が高速だとそれだけ深く読むことができ、強さにつながります。
開発の最初の段階ではまずバグなく実装すること、評価関数の精度を上げることが重要ですが、それらが一段落したら探索速度のチューニングを行うとよいでしょう。速度向上のためにはまず枝刈りを工夫することです。よりよいmove orderingを高速で実現するための手法を考えましょう。
チューニングのために、決まったテストケースを用意してベンチマークを行い、所要時間と探索ノード数の記録を取ります。探索ノード数から枝刈り性能が、nps(node per second: 1秒あたりの探索ノード数)から探索速度がわかります。探索ノード数を減らしつつ、npsを向上させることが重要です。ベンチマークは終盤探索向けと中盤探索向けの2つを用意して行うとよいでしょう。終盤/中盤共に高速化することが理想です。
打ち手の進行は違うのに、何手か先に同じ局面が現れる場合があります。局面が同じならばその局面の子孫の木は完全に同じになりますから、以前の探索の結果を再利用することで探索の効率を上げることができます。局面の状態と得点を保存しておくのが置換表(transposition table)です。
置換表は通常ハッシュテーブルとして実装されます。spotでは、オープンハッシュ(chainingによるハッシュテーブル)を用いています。置換表では、「要素の削除が起こらない(表全体のクリアはあるが、要素1つを取り出して削除することはない)」という前提がありますので、クローズドハッシュを用いるのもよいでしょう。また、ハッシュ値の衝突が起こったとき、両者を格納する努力をせず、既存のデータは上書きしてしまうという方法もあります。置換表の性質から、既存データを上書きしても効率が若干低下する可能性があるだけで、結果は変わらないからです。
ボードを識別するために何らかのハッシュ値を計算する必要があります。一般的なハッシュテーブルと同じく、ハッシュ値は計算が高速で、かつ異なった盤面は異なった値に変換されることが望ましいです。
spotでは、ボードが常に各辺のインデックスを保持していることを利用して、縦辺のインデックス8個(unsigned short * 8)を元にハッシュ値を計算します。具体的には、i番目のインデックスをindex[i]とすると
hash = sum(index[i] * 17^i)
という式で計算されます。17はアルファベット文字列をハッシュ化する際によいとされているマジックナンバーで、何となく用いてみたところそれまで使っていた手法に比べてハッシュ値の衝突が劇的に少なくなったため、採用しています。
置換表には以下のデータを入れています。
縦辺のインデックスが8個あれば、ボードの石の並びを一意に表現することができます。インデックス(0〜6560)は16ビットあれば十分表現できますので、16*8=128ビット+色情報、で局面を格納すればよいことになります。
注意すべきは格納する得点です。alpha-beta探索を行う場合、枝刈りによってノードの正確なminimax値が定まらないことがあります。このため、置換表にはそのノードが返す値を格納するだけでは不十分で、何らかの工夫を施す必要があります。1つの方法は、「真のminimax値が存在する範囲」を格納する方法です。真のminimax値とは、「alpha-betaカットをしなかった場合のminimax探索」においてノードにつく評価値のことです。もう1つの方法は、「値」とその「種類(真の値である/上限である/下限である)」を格納するものです。spotでは前者の「真の評価値が存在する範囲」を格納しています。つまり、「ボード」をキーとし、[上限, 下限]を値とするハッシュ表です。
探索の結果と真の評価値の関係は以下のようになります。
上限と下限が一致する場合を、「真の値が既に判明していること」の目印としています。
既に評価値の範囲がある程度わかっている局面に対してさらに探索を行い、新たに評価値範囲が得られたとします。このとき、真の評価値は「もともとわかっていた範囲」と「今回新たにわかった範囲」の共通部分に存在します。このようにして、探索を繰り返すうちに真の評価値が存在する範囲を絞り込んでいくことができます。未だ出現していない局面の評価値は(-∞, +∞)の範囲にあると考えます。
同一局面の再探索を防ぐのが置換表の役目、と書きましたが、実際のところ置換が起こりやすいと言われる終盤においても、置換表を使って削減できるノード数は全体の1/3程度です。置換表の役割は、むしろ反復深化などにおいて前回の探索で得られた情報を最大限利用する、ということの方が大きいのではないかと思います。
置換表を使う際は、探索木の上の方だけで使うようにすることに注意する必要があります。全てのノードを格納していては、かえって速度が低下しますし、深い探索においてはメモリを簡単に溢れさせてしまいます。
上に述べた「minimax値の存在範囲を格納する」タイプの置換表を用いた場合のalpha-betaアルゴリズムの擬似コードを示します。spotのコードでは、AI.cpp中のAlphaBetaAI::normal_alphabetaで完全な実装を見ることができます。(spotのコードはさらにnull window searchを組み合わせたアルゴリズムになっています。)
int alphabeta(int limit, int alpha, int beta)
{
if (limit == 0) return 評価値; // 深さ制限
現在の局面を置換表から検索して[上限, 下限]を取り出し; // 存在しなければ追加
// 以下、「上限」「下限」とはこの置換表から取り出した値のことをいう
if (置換表に存在) {
if (上限 <= alpha) return 上限; // alpha値を超えようがないので探索しても無駄
if (下限 >= beta) return 下限; // beta値を必ず超えてしまうので探索しても無駄
if (上限 == 下限) return 上限; // 既に真の値がわかっているので返す
// alpha-beta windowをなるべく狭くして効率up
alpha = max(alpha, 下限);
beta = min(beta, 上限);
}
/*
(本当はこのへんでパスかどうかの処理)
*/
int score;
int score_max = -∞; // このノードで出た最大値
int a = alpha;
全ての手を生成;
手をソート;
foreach (それぞれの手) {
手を打つ;
score = -alphabeta(limit-1, -beta, -a);
手を戻す;
if (score >= beta) {
// beta cut
置換表に[score, +∞)を追加; // 真の評価値は[score, +∞)のどこか
return score;
}
if (score > score_max) {
a = max(a, score);
score_max = score;
}
}
if (score_max > alpha)
置換表に[score_max, score_max]を追加; // 真の評価値はscore_maxと判明した
else
置換表に(-∞, score_max]を追加; // 真の評価値は(-∞, score_max]のどこか
return score_max;
}
(関数に渡された)alpha値と、「子ノードの最大値(score_max)」を区別することが重要です。子ノードの値がどれもalphaを越えなかった場合に差がでてきます。置換表に範囲を格納する際にこの2つを区別していないと、探索が正しく機能しません。また、子ノードの値がどれもalphaを越えなかった場合alphaを返すこととscore_maxを返すことを比較すると、後者の方がより真の評価値の範囲に近い情報を提供できるので、結果として枝刈りが多く発生し、探索が高速化されます。このような、なるべく多くの情報を探索の返り値として返す性質をfail-softであるといいます。
spotでは、かの有名なMichael Buro氏の論文"Experiments with Multi-ProbCut and a New High-Quality Evaluation Function for Othello"に示されたアイディアを用いて評価関数を実装しています。
spotの評価関数では、盤面の状態からそれ以降最善手を打った場合の最終的な石差を予想します。
IOSの対局から30万棋譜、Logistello's book skeltonの12万棋譜を合わせて使用。IOSの棋譜については終盤15〜17手の完全読み切りを行って棋譜中の誤りを訂正して使用しています。
spotでは以下の特徴(feature)を評価しています。それらの得点は、棋譜データ中の結果から回帰分析を行うことにより算出されます。
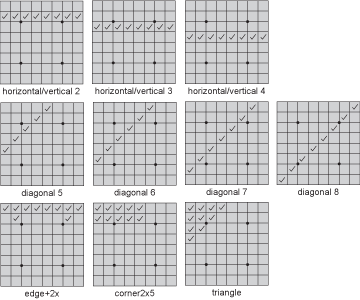
着手可能手数の近似値として、「ある辺に何カ所置けるか」という数値を用いています。この種の近似値は正確な着手可能手数を求めるのと比較して非常に高速で、かつよい近似を与えることが実験的に知られています。またspotにおいては、着手可能位置の評価は各パターンの評価値に事前に計算されて埋め込まれているので、着手可能位置の計算には実質コストがかかりません。
しかしながら、回帰分析を行うと、着手可能位置はゲーム序盤において有効な指針であるものの、20手目付近からどんどん結果への寄与が小さくなり、0に収束してしまうことがわかりました。これは、ゲームが後半に行くに従って棋譜中に出現するパターンの種類が増え、着手可能手数による優劣も含めてパターンの得点として説明されるようになる結果であると考えられます。
下図において、stageはリバーシの進行全60手を4で割った数値です。stage 13以降はほぼ0が続くため省略しています。縦軸は1カ所打てる場所があると何石差分有利かを示します。
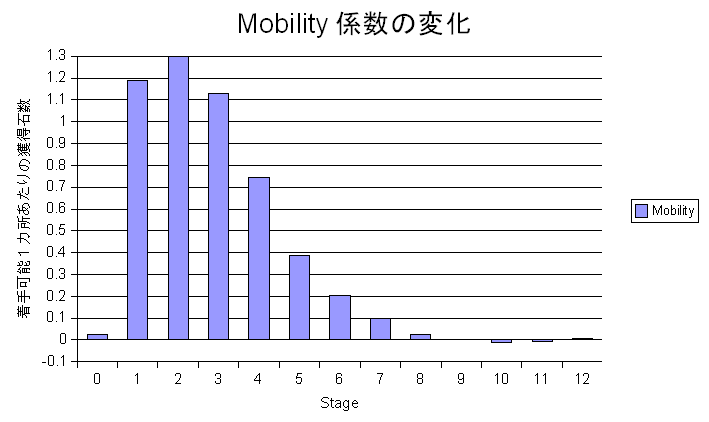
各パターンは一意なインデックスで識別されます。主要な縦・横・斜め辺のインデックスはボードが既に持っているので、評価関数ではそれらと、それらに多少周囲のマスを加えたインデックスを計算してテーブルから得点を読み、加算します。例えばedge2xパターンのインデックスであれば、horizontal/vertical 1のインデックスをボードが既に持っているので、それに2つのXの値を加えることで作ることが可能です。
また、着手可能手数の近似値として辺への着手可能数を見ていることから、着手可能手数による得点は辺の得点と見ることができます。このため、着手可能手数に関する得点は辺の得点に事前に埋め込むことができ、回帰計算による辺の評価値と、着手可能手数による評価値を合計して辺の得点とします。
さて、各パターンについて、得点を求める必要があります。具体的には例えば、「edge+2Xパターンのインデックス13102は何石分に相当するか?」という値を求めることになります。
この値は回帰分析によって求めます。教師信号となる棋譜データに対して、評価関数が予想する値と実際の結果との誤差の二乗が最小になるようにパラメータを調整してやるわけです。説明変数が数十万個にのぼるため、最急降下法を用いて段階的に調整していくことになります。
最急降下法はしばしば局所解に陥りやすいとして欠点が指摘されますが、リバーシの評価関数においては(経験的事実ですが)全ての初期値を0として学習をはじめれば妥当な評価関数ができあがります。
評価関数の学習については、こちらの文書も参考にしてください→リバーシの評価関数の最適化
序盤は有利となる配置でも、終盤においても同様に有利であるという保証はありません。このため、リバーシの進行全60手を4手ごとに区切って15ステージに分け、ステージごとにそれぞれのパターンの評価値を求めます。
また、パターンによっては左右対称あるいは回転対称といった対称形が存在します。対称なパターンには当然同じ評価値がつくべきであるという考えに基づき、学習時には全部のパターンを対称形のうちインデックスの値が小さい方に正規化してカウントし、最後にインデックスが大きい方にもその学習結果をコピーしています。このようにすることで、「対称形に同じ得点がつく」という効果の他に「各パターンの出現頻度を多くすることができ、学習の信頼度が高まる」という効果が得られます。
ステージ分けの結果、ステージが変わると評価値が大きく変わるということが考えられます。手数にして1手分しか変わらないのに、評価値が大きく異なることは考えにくいことです。この問題を解決するために、本来そのステージにカウントされる4手分の棋譜の他に、本来は隣接したステージに属する手数の局面も併せて合計6手分の局面を入力として学習を行っています。
(あとでちゃんと書く)
(あとでちゃんと書く)
当然ながら棋譜中に全く出現しなかったパターンについては評価のしようがありませんので、0点とせざるを得ません。しかしながら本当はその並びはとてもよい並びであるかも知れず、逆にとても悪い並びである可能性もあります。そのために、局面の評価を誤る可能性もあります。
「棋譜中に出現しなかったパターンはそもそも重要度が低いので関係ない」という考え方もありますが、広大なゲーム木探索空間の中には相当異常な手も含まれており、(双方がそれなりにまともな手を打つことが多いと思われる)棋譜からでは学習できない局面が存在する可能性も否定できません。
この問題を解決するための方法として、すでに得点のわかっているパターンを使って石の並びから得点を予想するニューラルネットワークを構築し、それを用いて未知のパターンの得点を予想するという手法がKeyanoの作者によって提案されています。
学習の結果できあがった評価関数が果たして以前よりもよくなったのか悪くなったのか、きちんと評価する必要があります。評価関数の評価のためには、評価関数を柔軟に取り替えられるように思考ルーチンを設計しておき、異なる評価関数同士を戦わせて勝敗を見ます。
具体的には、random opening、つまり最初の数手をランダムに打った時点から試合をはじめます。1つのopeningについて先手・後手を入れ替えて2試合を行います。これを、100openingもしくは1000opening程度の多くの局面に対して行います。膨大な試合をこなす必要があるため、クラスタ等の環境があると便利です。各試合は完全に独立なので、各CPUにジョブを投げて並列に実行させることができます。
評価の原理はこうです。random opening後の局面が与えられた時点で、双方が最善を打った場合の勝敗は決しているはずです。よって2つの評価関数が同じ強さだとしたら、全試合中の勝ちと負けの回数が同数になるはずです。勝ち負けの回数の偏りを見ることで、どちらの評価関数がよいかを判断します。 その差が有意なものであるか、ただ数字を見るだけではなく、統計的に検定を行うことが必要です。
定石は序盤の打ち間違いを防いで不利な展開に陥るのを防ぎ、また定石に乗っている間は探索が不要なため高速化にも貢献します。持ち時間一定の対局の場合は定石を用いることで、それ以降の中盤〜終盤により多くの時間を割けるようになります。
しかしながら、現在のThellはまだ定石を実装していません。これは、Thell3開発の動機となった学科内オセロプログラミングコンテストにおいて定石の使用が禁じられていたこと、実装する余裕がなかったこと、また定石を自分で生成できるようなシステムを構築したいと考えていること、等の理由によります。
Thellの実装にあたって、多くの方々の助言によって様々なアイディアを得たり、議論を深める中で新しいアイディアを生み出したりすることができました。感謝の意を込めて、ここに記したいと思います。
Copyright (C) 2001-2007 Seal Software <sealsoft AT sealsoft.jp>